3D object를 2D에 적절한 size, position, orientation 표현하기 위해서는 Intrinsic/Extrinsic parameter를 알아야 한다. Calibration은 해당 parameter를 구하는 과정이다.
Camera lens system
1. Pinhole camera

2. Modified camera

| Focal length | Distance between lens and image plane |
| Principal point | Where optical axis meets image plane |
Camera paramter
1. Intrinsic

2. Extrinsic

카메라의 position과 orientation을 말한다.
Parameter는 항상 일정하지 않기 때문에 calibration을 통해서 알맞은 parameter를 찾아내서 사용해야 한다.
3D-2D projection
다음의 식을 이용해서 구할 수 있다.
q = MQ

q = sMWQ

Homography
planar projective transformation.

Unknown이 8개이므로 관련된 식이 8개 필요하다. Homography를 구하는 방법은 다음과 같다.
1. Get Homography using "q = HQ"
Sample point에 대해 다음의 식을 얻을 수 있다.

이를 통해서 sample point를 다음과 같이 정의할 수 있다.

이로써 sample point 1에 대해서 H와 관련된 식 2개를 얻을 수 있음을 알 수 있다. 따라서 unknown이 8개이므로 총 4개의 sample point를 가지고 있다면 homography를 구할 수 있게 된다. 위 식을 행렬식으로 변환하면 다음과 같이 나타낼 수 있다.

정확히 4개의 point를 이용해서 homography를 구할 수 있다. 하지만, 현실에서는 이보다 많은 점을 이용해 homography를 구하게 된다. 오차가 있을 수 있기 때문이다.
2. Homography decomposition using "q = HQ = sMWQ"
내부 parameter를 구하기 위해서는 위에서 구한 homography를 intrinsic/extrinsic parameter로 분해해줘야 한다. "q=HQ=sMWQ"이므로 "H=sMW"이다.

$[h_{1} h_{2} h_{3}] = sM[r_{1} r_{2} t]$
then we have
$h_{1} = sMr_{1}, h_{2} = sMr_{2}, h_{3} = sMt$
$r_{1} = {M^{-1} \over s}h_{1}, r_{2} = {M^{-1} \over s}h_{2}, t = {M^{-1} \over s}h_{3}$
2-1. $r_{1}$ and $r_{2}$ are orthogonal
$r_{1}^{T}r_{2} = 0$
$({M^{-1} \over s}h_{1})^{T} {M^{-1} \over s}h_{2} = 0$
$h_{1}^{T}(M^{-1})^{T}M^{-1}h_{2} = 0$ ... (1)
2-2. $|r_{1}| = |r_{2}| = 1$
$M^{-1}h_{1} = M^{-1}h_{2}$
$h_{1}^{T}(M^{-1})^{T}M^{-1}h_{1} = h_{2}^{T}(M^{-1})^{T}M^{-1}h_{2}$
$h_{1}^{T}(M^{-1})^{T}M^{-1}h_{1} - h_{2}^{T}(M^{-1})^{T}M^{-1}h_{2} = 0 $ ... (2)
2-3. Let B = $(M^{-1})^{T}M^{-1}$

B는 Intrinsic parameter에 관한 식으로 이루어져 있어 B를 알면 intrinsic parameter를 구할 수 있다. $(M^{-1})^{T}M^{-1}$을 전개해 보니, symmetric임을 알 수 있다. 따라서 B의 unknown은 6개가 된다. 그리고 위의 조건들로부터 얻은 식 2개((1), (2))를 정리하면 하나의 homography로부터 2개의 식을 얻을 수 있음을 확인할 수 있다.


따라서 총 3개의 homography(=image)가 있으면 intrinsic parameter를 구할 수 있게 된다. 여기도 마찬가지로 실제로는 3개 이상의 image를 사용하게 된다.
Extrinsic parameter는 위에서 구한 $r_{1}, r_{2}, r_{3} = r_{1} \times r_{2}, t$를 통해서 구할 수 있다.
Camera Distortion
- Radial distortion
- Tangential distortion
Radial distortion
Lens가 spherical이어서 발생하는 문제이다. Taylor series를 이용해서 보상해준다.
$x_{corrected} = x(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6}+...)$
$y_{corrected} = y(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6}+...)$
일반적으로 $k_{2}$까지 사용한다.
Tangential distortion
Lens와 CCD가 평행하지 않아서 발생하는 문제이다. $p_{1}, p_{2}$를 이용해서 보상해준다.
$x_{corrected} = x + [2p_{1}xy + p_{2}(r^{2}+2x^{2})]$
$y_{corrected} = y + [p_{1}(r^{2}+2y^{2}) + 2p_{2}xy]$
Distortion coefficients
$x_{p} = x_{d}(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6}) + [2p_{1}x_{d}y_{d} + p_{2}(r^{2}+2x^{2}_{d})]$
$y_{p} = y_{d}(1+k_{1}r^{2}+k_{2}r^{4}+k_{3}r^{6}) + [p_{1}(r^{2}+2y^{2}_{d}) + 2p_{2}x_{d}y_{d}]$
Intrinsic parameter를 이용해서 $x_{p}$와 $y_{p}$를 구해서 unknown $k_{1}, k_{2}, k_{3}, p_{1}, p_{2}$를 찾으면 된다. Unknown이 5개이므로 점 3개가 있으면 구할 수 있다.
*pinhole camera의 $x_{p}, y_{p}$

Calibration Procedure
- Homography for each images
- Camera prameter
- Distortion coefficient
- Repeat
- Get compensated point
- Update Parameter
- Get Distortion coefficient
Re-projection Error
$\varepsilon = \sum ||p-q'||$, q'=sMWQ
Augmented Reality

- Camera calibration
- Intrinsic parameter 구하기
- 다른 pose의 여러 이미지 사용
- Finding corner points of marker
- Estimation of Marker Pose
- marker의 position, orientation 찾기
- Finding homography
- Finding pose
- Projection to Image phase
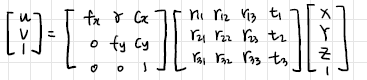
'대학교 > 컴퓨터비전' 카테고리의 다른 글
| [CS/컴퓨터비전] 11. Deep Learning (0) | 2022.06.12 |
|---|---|
| [CS/컴퓨터비전] 9. Homogeneous Transformation Matrix (0) | 2022.06.11 |
| [CS/컴퓨터비전] 8. Fourier Decriptor (0) | 2022.06.11 |
| [CS/컴퓨터비전] 7. Bayes Classifier (0) | 2022.06.11 |
| [CS/컴퓨터비전] 6. Object Recognition (0) | 2022.06.11 |
