Template Matching
Kernel을 통해서 pattern이 있는지 찾는 방법이다. Filter와 Image가 유사할수록 큰 값을 가진다.
$c(x,y) = \sum_{s} \sum_{t} \omega(s,t) f(x+s, y+t)$
Normalization할 수 있다.
$c(x,y) = {\sum_{s} \sum_{t} [\omega(s,t) - \omega_{mean}] [f(x+s, y+t)-f_{mean}] \over \sum_{s} \sum_{t} [\omega(s,t) - \omega_{mean}]^{2} [f(x+s, y+t)-f_{mean}]^{2}}$
size와 rotation의 normalization은 복잡해서 다른 방법이 필요하다.
*2D rotation

Linear Interpolation&Extrapolation

- Interpolation : 확대했을 때, hole이 생기는데 이 hole의 값을 predict할 때 사용한다. 여러 보간법이 존재한다.
- Extrapolation : 축소했을 때, 사용된다.
Fourier Descriptor
Object의 size와 rotation 파악할 때 쓰는 것으로, Pre-processing의 목적으로 주로 사용된다.
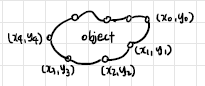
$s(k) = x(k) + i y(k)$
Fourier Transform...
$a(u) = \sum_{k=0}^{N-1} s(k) exp(- {2\pi uk \over N})$
u는 object's curve의 frequency라고 보면 된다. 따라서 u가 작으면 approximated shape에 관한 정보이고 u가 크면 detailed shape를 표현한다. 구체적인 정보는 다음과 같다.
| a(0) | position of center of gravity translation infromation |
| a(1) | size of the shape alone = shape is circle, r = a(1) scaling information |
| Phase | rotation of this perturbation show where the action is performed on a(1) circle |
| Others | a(1) circle에 자잘한 변화(alteration)를 줌 |
| Negative value | positive와 opposite effect |
Fourier descriptor로 할 수 있는 것은 Translation, Scaling, Rotation이며 모르는 것은 Object의 Position, Size, Orientation이다. 모르는 부분은 뒤에서 배우는 Homography를 통해서 알 수 있다.
Pre-processing
Translation : $a(0) = 0$
Scaling : $a'(u) = a(u) / a(1)$
Rotation Invariance : $a'(u) = a(u) / ej^{\phi}$
'대학교 > 컴퓨터비전' 카테고리의 다른 글
| [CS/컴퓨터비전] 10. Camera Calibration (0) | 2022.06.11 |
|---|---|
| [CS/컴퓨터비전] 9. Homogeneous Transformation Matrix (0) | 2022.06.11 |
| [CS/컴퓨터비전] 7. Bayes Classifier (0) | 2022.06.11 |
| [CS/컴퓨터비전] 6. Object Recognition (0) | 2022.06.11 |
| [CS/컴퓨터비전] 5. Segmentation (0) | 2022.06.11 |
