[CS/컴퓨터비전] 3. Filtering in Frequency Domain

Background - Fourier Trasnform

use of sinusoids to represent temperature distribution

 

Any continuous periodic signal can be expressed as the weighted sum of sine and cosine waves.

weighted sum of simusoids

 

Fourier Transform

Fourier Transform

Time domain과 Frequency domain의 전환은 위와 같다. 

 

concept

Background의 설명처럼, 어떤 신호도 주기성을 가지는 함수의 조합으로 나타낼 수 있는 점을 이용해, 우리는 신호를 분해할 수 있다. 그림처럼, 어떤 신호가 동일한 주기성을 가지는 sin함수와의 곱을 적분하면, 0이 아닌 값을 가지게 된다. 

 

다른 한편, cosine의 역할은 주기의 delay를 나타내는 데 사용된다.

role of cos

 

Fourier Transform Group

FT group

 

Discrete Fourier Transform, DFT

Input: finite sequence of real or complex numbers

DFT and IDFT

 

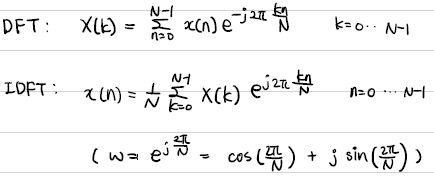
Fourier Transform

FT

 

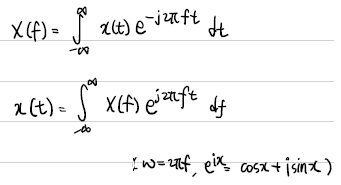
2D DFT for Image

2 dimension DFT

---

Low Pass Filter

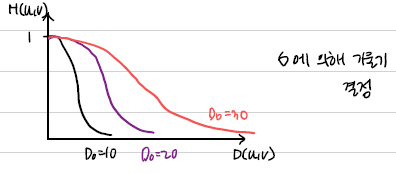
Ideal Low Pass Filter, ILPF

ILPF

Smoothing filter이다. High frequency 차단으로 인해 IFT시 "ringing effect"를 야기한다. 노이즈 제거에 사용된다.

ILPF

 

Butterworth Low Pass Filter, BLPF

BLPF

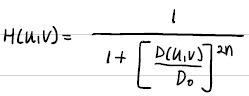
ILPF보다 부드러운 Smoothing을 할 수 있다. n이 클수록 sharp 해진다. ILPF와 마찬가지로, "ringing effect"가 발생한다.

BLPF

 

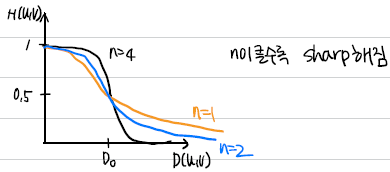
Gaussian Low Pass Filter, GLPF

GLPF

Tight control이 필요하면, ILPF와 BLPF를 사용한다. GLPF는 tight하지는 않다. 대신 ringing effect가 없다.

GLPF

 

---

High Pass Filter

HPF

Ideal, Butterworth, Gaussian

---

Centering

1차원에서 FT 결과는 다음과 같이 나타날 수 있다.

result of FT

M 주기를 가지도록 표현하고 싶다. $f(x)(-1)^{M/2}$

Center에 저주파 성분이 모이게 되었다.

 

이미지에도 적용할 수 있다.

centering of Image

 

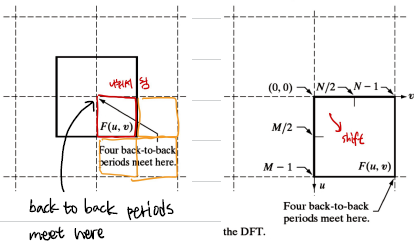
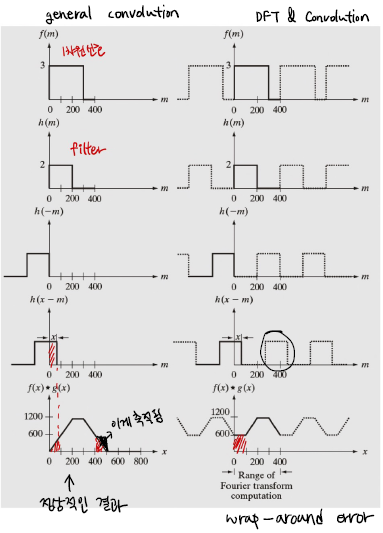
Inherent Periodicity Problem

함수들이 주기성을 가지기에 Inf 반복해서 신호가 나타나는 것처럼 계산이 된다. 이런 현상에 의한 원치 않는 축척의 결과를 wrap-around error라고 하며 이를 방지하기 위해, zero padding이 필요하다.

General convolution and DFT+convolution